この記事はグラフ作成編の続きです。petgraphでグラフを作成する方法をお探しの方はこちらをご覧ください。
この記事はAtCoderで使用することを前提で記載していますので、petgraphのバージョンは0.5.0を使用します。しかし、rustではセマンティックバージョニングを使用しているので、petgraphの0.*.*であれば適用可能だと思います。
この記事で書くこと
petgraphを用いて、以下の2つの基本的なグラフ探索を行います。
ここに出てくるコードでは、以下を使ってpetgraphモジュールを使用しています。
use petgraph::prelude::*;
また、この記事では以下のグラフに対して探索を行います。
petgraphを用いてグラフを作成する方法についてはこちらをご参照ください。
let es = [(0,1),(1,2),(1,3),(3,4),(0,5)];
let graph = Graph::<(),(), Undirected>::from_edges(es);

petgraphを用いた深さ優先探索(DFS)
petgraphを用いてDFSを行います。
ちなみに、深さ優先探索については、分かりやすい記事があります。
DFS (深さ優先探索) 超入門! 〜 グラフ・アルゴリズムの世界への入口 〜【前編】
DFS実装
let mut dfs = Dfs::new(&graph,NodeIndex::new(0));
let mut dfs_order = vec![];
while let Some(node) = dfs.next(&graph) {
dfs_order.push(node.index());
}
println!("{:?}",dfs_order);
実行結果
[0, 1, 2, 3, 4, 5]
コード解説
petgraph::visit::Dfsのnewメソッドを使ってdfsインスタンスを作成します。newの引数には、Graphインスタンスの参照とNodeIndexのインスタンスが必要です。上記の例では、「インデックスが0のnodeからdfsを始める」の意味になります。
続いて、以下のコードでdfs.next()からNoneが返ってくるまでnextを続けます。
while let Some(node) = dfs.next(&graph)
内部挙動
dfsインスタンスは、構造体で、その要素にstackとdiscoveredを持っています。
stackは「どのノードを見るか」というtodoリストになっています。discoveredは「ノードを探索したか」という探索の結果になっています。
上記のコードとこれらの動きをみてみます。
グラフを作るとき
let mut dfs = Dfs::new(&graph,NodeIndex::new(0));
dfsのインスタンスは以下のようになっています。

次のノードを探索するとき
dfs.next(&graph)
dfsのnextメソッドにはの裏ではいくつかの動作が行われています。
stackから次に巡るNodeIndexを取り出す
要素が複数ある場合は、最後に入れたものを取り出します。
以下の図では上にある方が優先です。
stackに要素がなかったらNoneを返します。

取り出されたNodeIndexが未発見であれば、そのNodeIndexのdiscoveredをtrueにする
発見されていれば、「stackから次に巡るNodeIndexを取り出す」に戻ってやり直します。
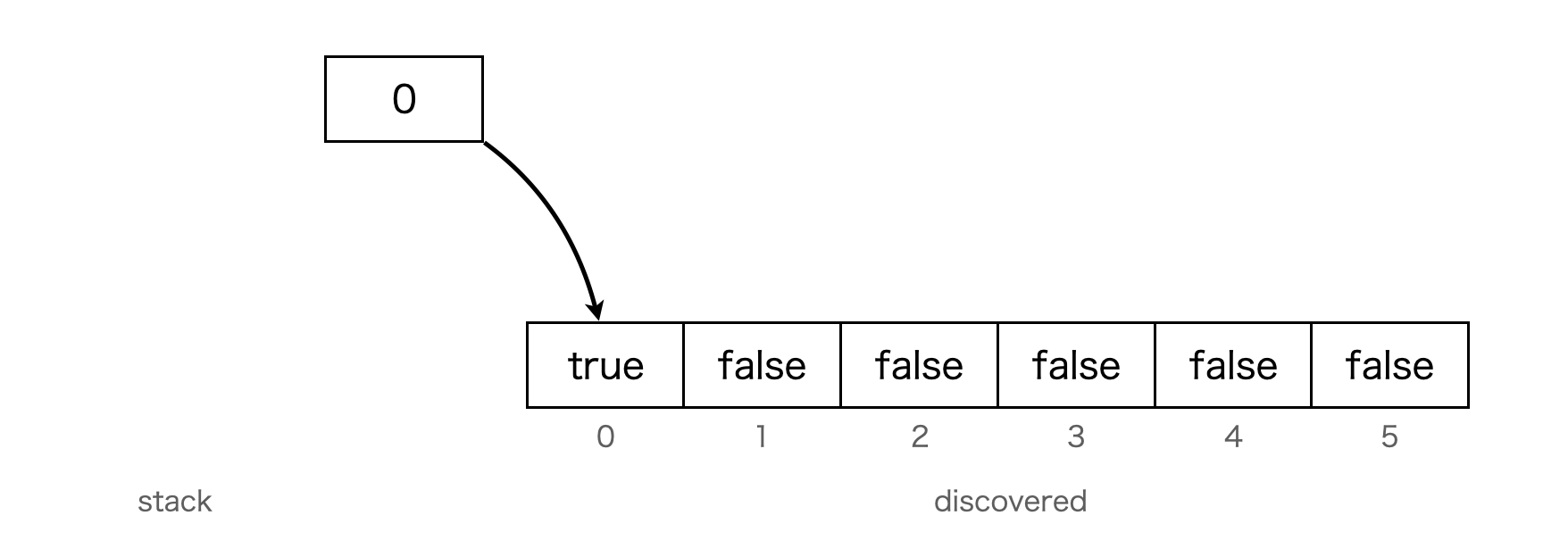
Graphインスタンスの中から、未発見だったNodeIndexのお隣さんを見て、お隣さんも未発見ならstackに追加する
今回のグラフでは1と5がお隣さんです。
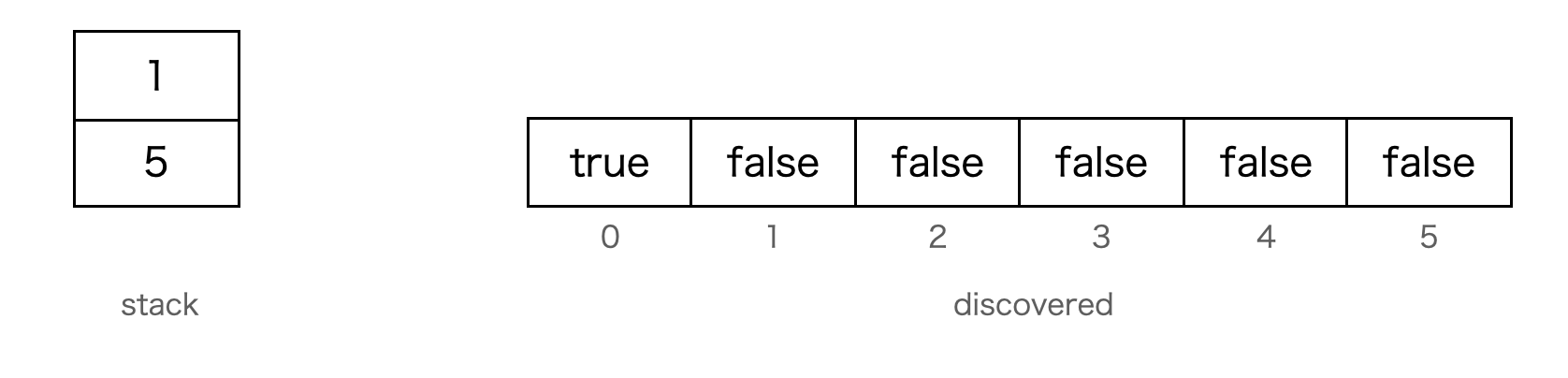
NodeIndexを返す
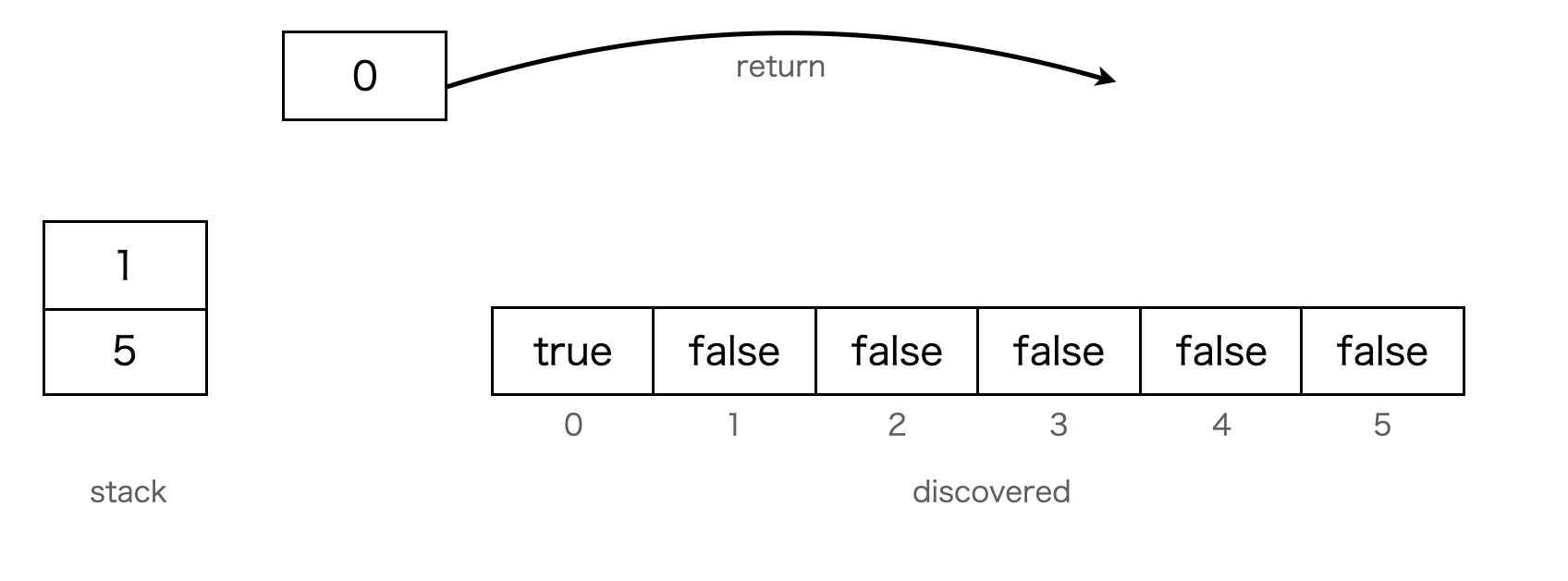
以上のようにして、グラフの探索を行ってくれます。
実際に探索の途中でdiscoveredがどうなっているか見てみます。
ここでは、while let文の中でdfs.discoveredの中を表示させます。
ちなみに、AtCoderで使えるpetgraphのバージョン0.5.0では、discoveredの配列を一つ一つ見ていくしかありませんが、最新バージョンではprintln!(“{:b}”,dfs.discovered);で表示できます。
これはdfs.discoveredが使用しているFixedBitSetクレートが0.3.0からBinaryトレイトを実装したからです。petgraphの0.5.0はFixedBitSetの0.2.0に依存しています。
let mut dfs = Dfs::new(&graph,NodeIndex::new(0));
let mut dfs_order = vec![];
while let Some(node) = dfs.next(&graph) {
for i in 0..dfs.discovered.len() {
if dfs.discovered[i] {
print!("{}",1);
}else {
print!("{}",0);
}
}
println!();
dfs_order.push(node.index());
}
実行結果
100000
110000
111000
111100
111110
111111
深さ優先探索なので、今回の場合NodeIndexが0から順番に探索されています。
これはdfsのstackの型がVecのpopとpushで動作しているからです。
これにより、いわゆる「スタック」の動作を実現しています。
petgraphを用いた幅優先探索(BFS)
petgraphを用いてBFSを行います。
と言っても、DFSと流れは全く同じです。違いはDfsがBfsになったことのみです。
let mut bfs = Bfs::new(&graph,NodeIndex::new(0));
let mut bfs_order = vec![];
while let Some(node) = bfs.next(&graph) {
bfs_order.push(node.index());
}
println!("{:?}",bfs_order);
実行結果
[0, 5, 1, 3, 2, 4]
内部挙動
bfsのインスタンスはdfsと同じく、stackとdiscoveredを持っています。しかし、stackという名前ですが、VecDeque型であり、お隣さんを追加するときは、pop_frontとpush_backメソッドで動作します。これで、いわゆる「キュー」の動作を実現しています。
また、stackへのノード追加のタイミング等もDfsと異なっています。
グラフを作るとき
let mut bfs = Bfs::new(&graph,NodeIndex::new(0));
Bfs::newでグラフを作成した後、bfsインスタンスは以下のようになっています。
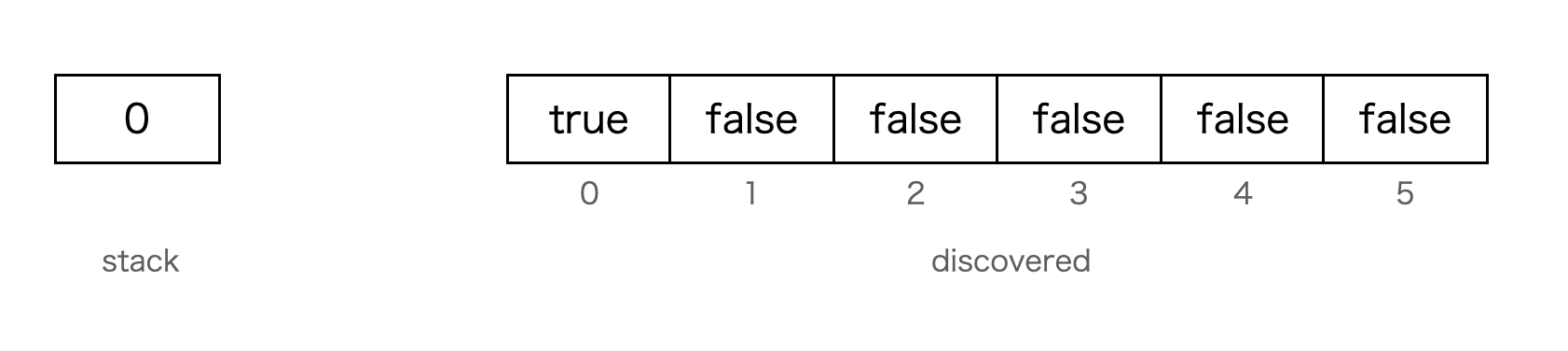
探索の始めのノードのインデックスをstackに追加し、それに対応するdiscoveredの配列要素をtrueにします。
ここでは0を最初のインデックスに指定したので、stackに0を追加し、discovered[0]をtrueにします。
dfsの時はstackに0を追加するだけでしたが、bfsではそれに加えて、discovered[0]をtrueにします。
次のノードを探索するとき
bfs.next(&graph)
stackから次に巡るNodeIndexを取り出す
要素が複数ある場合は、先に入れたものを取り出します。
以下の図では下の方にある方が優先です。

お隣さんをgraphインスタンスから見つけ、それらのNodeIndexが未発見なら対応するdiscoveredの要素をtrueにして、stackに追加する

NodeIndexを返す

以上のようにしてグラフの探索を行ってくれます。
内部の動作を見ると、DfsとBfsではdiscoveredをtrueにするタイミングが違います。
あるNodeIndexに対して、discoveredをtrueにするタイミングは、以下のようになっているようです。
- Dfs -> お隣さんを全てスタックに入れたら
- Bfs -> スタックに入れられる前
なぜこのような実装になっているのか、理解できていないです。Dfsにするか、Bfsにするかは、それぞれスタックを使うかキューを使うかで決まると思っています。なのでアルゴリズムに変更は不要だと思います。メモリ効率が関係していると推測していますが、詳細はよく分かりません。
dfsの時と同様に、discoveredを見てみます。
let mut bfs = Bfs::new(&graph,NodeIndex::new(0));
let mut bfs_order = vec![];
while let Some(node) = bfs.next(&graph) {
for i in 0..bfs.discovered.len() {
if bfs.discovered[i] {
print!("{}",1);
}else {
print!("{}",0);
}
}
println!();
bfs_order.push(node.index());
}
実行結果
110001
110001
111101
111111
111111
111111
bfsの内部挙動のところの図にあるように、1回目のnextを実行した段階でdiscoveredは110001になります。
この時のNodeIndexは0です。
次のnextでは、NodeIndexは5になりますが、未発見のお隣さんはいないため110001のままです。
次のnextでは、NodeIndexは1になり、未発見のお隣さん2,3を見つけ、stackに追加します。
…
のような挙動でこのような実行結果になっています。
最後に
petgraphを用いたDFS,BFSについては以上です。
これでとりあえず探索はできるようになりました。
次はもう少し発展的なアルゴリズムとして、petgraphのalgoモジュールを使って、dijkstraや二部グラフ判定を行います。
ご覧いただきありがとうございました。



コメント